Arme maîtresse pour tout joueur qui se respecte, le service est primordial si l’on veut dominer l’échange. On a souvent associé grand joueur (par la taille) avec grand service, je me suis « amusé » à tenter de vérifier cette légende urbaine par une étude mécanique… Je vais donc essayer de faire le plus simple possible pour ne pas perdre les allergiques aux maths et à la physique !
Pour ce faire, j’ai du prendre plusieurs hypothèses :
- On se place dans un cadre avec un vent nul, en indoor par exemple,
- On prendra pour modèle un joueur d’1m80 frappant ainsi à 2m80 de hauteur (bras + longueur de raquette + poussée des jambes),
- On considèrera un service à plat, on ne tiendra donc pas compte ici de la rotation propre de la balle qui entraînerait des effets aérodynamiques difficiles à prendre en compte dans l’étude,
- On ne tiendra pas compte de la déformation de la balle suite au choc,
- On ne s’aventurera pas non plus à quantifier l’influence du fait que la balle ne soit pas lisse, qui obligerait à prendre de nouvelles variables en compte.
Le but est triple : prévoir la trajectoire de la balle, l’évolution de sa vitesse entre la frappe et l’instant précédent le choc avec le sol et comparer ces deux critères suivant la taille du serveur.
Première partie : Service « au T »
Pour plus de simplicité prenons le cas d’un serveur droitier, servant de gauche à droite. La trajectoire de la balle est quasiment rectiligne, c’est-à-dire que la balle ne varie que dans 2 dimensions (la trajectoire ne varie pas en largeur, contrairement à un service plus croisé).
1er cas : Chute libre (frottements nuls)
Juste après le choc avec la raquette, la balle subit une seule force, son propre poids, autrement dit l’attraction du centre de la Terre qui fait tomber tout objet non retenu.
En réalité l’atmosphère crée une 2ème force, de frottement, qui s’oppose au déplacement de la balle. On le verra dans le 2ème cas.
Si on appelle alpha l’angle initial que fait la trajectoire de la balle avec la verticale, on peut mettre en équation cette trajectoire en utilisant le Principe fondamental de la dynamique (PFD) : m*a = P (1)
m : masse de la balle (57g)
a : accélération de la balle
P : poids de la balle
En projetant l’équation (1) sur les axes y et z reliés respectivement à la longueur du terrain et à l’altitude, et en intégrant, on obtient l’expression de la vitesse sur y et sur z :
Vy(t) = v0*sin(alpha) (2)
Vz(t) = -g*t – v0*cos(alpha) (3)
v0 : vitesse initiale de la balle, c’est-à-dire après sortie de raquette, on prendre 200km/h (55,5m/s)
g : accélération de la pesanteur (9,81 m/s^2)
t : variable du temps
On intègre une seconde fois pour avoir le déplacement sur les deux axes :
Y(t) = v0*sin(alpha)*t + y0 (4)
Z(t) = -0.5*g*t^2-v0*cos(alpha)*t+z0 (5)
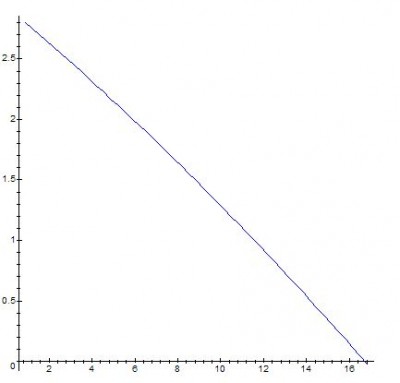
Le graphe ci-dessus donne l’altitude de la balle en fonction du déplacement sur la longueur du terrain. Par exemple à y=y0=0,9m, la balle est à 2.8m d’altitude (instant initial). En effet, j’ai considéré que le serveur ne tapait pas la balle au niveau de la ligne de font de court mais à 0.9m en aval (poussée des jambes vers l’avant).
A y=16.58m, on a z=0, en d’autres termes c’est à cette longueur que la balle touche le sol.
Pour valider le modèle, il faut s’assurer que la balle passe évidemment au-dessus du filet, on va donc jouer sur l’angle alpha décrit précédemment afin d’être « juste » au dessus du filet, on minimise ainsi la durée de déplacement de la balle pour maximiser l’efficacité du service. Numériquement on trouve pour l’exemple du joueur d’1m80, alpha=81,3°.
Puis on obtient la vitesse globale en calculant la norme avec les relations (2) et (3).
On va ainsi avoir une vitesse qui augmente constamment au cours du temps, ce qui est impossible. Ce modèle est donc faux !
On doit prendre en compte un facteur d’amortissement, en clair l’existence de frottements due à l’atmosphère dans laquelle évolue notre balle de tennis.
2ème cas : Présence de frottements fluides linéaires
Si on lâchait une balle de tennis du haut de la tour Eiffel, on remarquerait que sa vitesse se stabilise rapidement autour de 60 km/h. Cette vitesse limite est due à notre atmosphère qui freine l’objet. Ainsi, si le service part à 200km/h, il est évident qu’il aura perdu en vitesse entre le moment où le serveur frappe et l’instant où la balle touche le sol. La durée étant de l’ordre de 0.3 secondes, quelle est la vitesse réelle de la balle juste avant de toucher le sol ?
L’étude se décompose de manière similaire au 1er cas, on doit néanmoins tenir compte de la force de frottement, qui intervient dans l’écriture du PFD. Cette force est proportionnelle à la vitesse de la balle (plus la balle va vite, plus elle sera freinée). D’où l’équation :
m*a = P + k*v (6)
où v désigne bien sûr la vitesse et k le coefficient de frottement fluide.
On projette comme avant sur les deux axes et on obtient des équations différentielles.
Passés les calculs on obtient :
Vy(t) = v0*sin(alpha)*exp(-(k/m)*t) (7)
Vz(t) = ((m*g)/k-v0*cos(alpha))*exp(-(k/m)*t) – (m*g)/k (8)
Passons ces expressions assez imbuvables et intéressons-nous plutôt au graphique représentant la vitesse en fonction du temps :
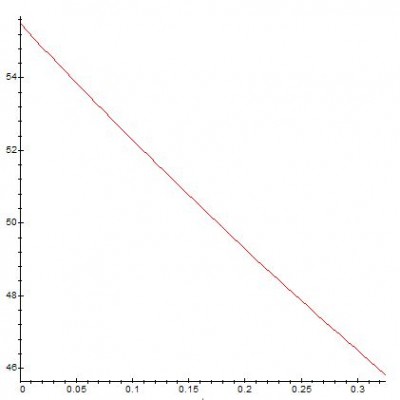Entre le moment où la balle sort de la raquette et son impact avec le sol (un peu plus de 0.3 secondes), la vitesse a diminué de 9,4m/s, soit près de 34 km/h. Beaucoup en 3 dixièmes de seconde, mais pas impossible vu la masse (assez légère) de la balle de tennis. Une balle de pétanque, par exemple, aurait été beaucoup moins freinée.
L’intégration des relations (7) et (8) nous donnent les équations paramétriques du mouvement (trajectoire) :
Y(t) = -(m*v0*sin(alpha))/k*exp((-k/m)*t) + (m*v0*sin(alpha))/k + y0 (9)
Z(t) = -((m/k)*((m*g)/k – v0*cos(alpha)))*exp(-(k/m)*t) – (m*g)/k*t + (m/k)*((m*g)/k – v0*cos(alpha)) + z0 (10)
Et comme on est en présence de frottements, l’angle alpha trouvé dans le 1er cas n’est plus suffisant pour être juste au-dessus du filet. Il faut donc l’augmenter légèrement (alpha=81.4°). Ainsi la vitesse diminue légèrement aussi.
On peut alors avoir les 2 trajectoires sur un même graphique, celle avec frottements (2ème cas) et celle sans frottements (1er cas) :
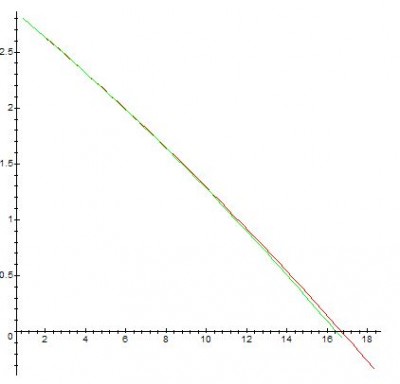La courbe rouge représente le 1er cas, la verte le cas avec frottements. On remarque que la verte est légèrement en retrait de la rouge. En d’autres termes, pour des conditions identiques (même serveur, même vitesse initiale), la balle faisant face à des frottements touche le sol avant (16.44m) celle à l’état « libre » (16.58m). Pour un même intervalle de temps on remarque également que la balle « libre » est déjà bien plus en avance que celle subissant les frottements (la verte touche à peine le sol lorsque la rouge est déjà « enfoncée » dans le sol).
Ces observations confirment donc que les frottements de l’atmosphère jouent un rôle, assez minime pour la trajectoire, mais loin d’être négligeable pour la vitesse de la balle et la durée du service…
C’est l’angle alpha qui va faire toute la différence entre un petit et un grand serveur.
Pour un serveur plus petit que notre serveur de référence, il va falloir augmenter alpha, et inversement pour un grand serveur.
Prenons deux cas extrêmes : Olivier Rochus : 1m68. Il va frapper la balle à environ 2m50 (j’ai tenté de mesurer cela sur les vidéos youtube). Deux contraintes s’imposent : passer par-dessus le filet (0.914m) et ne pas dépasser la ligne de service en longueur située à 18.29m du joueur.
Pour une vitesse en sortie de raquette de 200km/h, en calculant l’angle minimum nécessaire pour être au-dessus du filet (alpha=83°), on trouve une position d’impact à 17,09m du joueur, atteinte au bout de 325 ms (milisecondes).
Prenons à présent un joueur très grand, par exemple Ivo Karlovic : 2m08. Il devrait frapper la balle à environ 3m30. Ainsi mes calculs (alpha=79°) montreraient qu’il peut aisément frapper à 200km/h juste au dessus du filet avec une marge bien plus grande… En effet, l’impact se produirait à 15,61m, soit près d’1m50 avant la balle de Rochus et cela au bout de seulement 216 ms, environ deux tiers du temps mis par le Belge !
On peut même aller beaucoup plus loin en terme de vitesse, ainsi avec les hypothèses prises, la taille du géant Ivo lui permettrait de réussir un service à plus de 350 km/h dans les limites du court ! Evidemment les limites humaines interviennent alors, mais malgré mes hypothèses prises en début d’étude, je ne trouve pas inenvisageable l’idée d’un robot placé à 3.3m de hauteur tirant des services à 350km/h…
D’ailleurs, l’angle alpha par rapport à la verticale étant plus grand pour le Belge, il en résulterait une baisse de vitesse, néanmoins, vu le court intervalle de temps, cela n’influence quasiment pas.
Rochus est rassuré, il peut donc à priori servir à 200km/h, néanmoins il est évident qu’un serveur comme Karlovic, de par sa taille, maximise ses chances de réaliser un service gagnant grâce au gain de temps (33%) qu’il obtient sur le Belge. Le fait que la balle rebondisse dans une zone plus courte ne constitue pas un réel avantage pour un service « au T ». En revanche, il est clair qu’il aura toute son importance pour un service croisé extérieur !
Voilà, l’étude est longue pour un résultat finalement assez attendu, mais je trouve intéressant de pouvoir modéliser ce type de « phénomène » assez simple en apparence.
3ème cas : Présence de frottements fluides quadratiques
A partir de certaines vitesses trop élevées, la force de frottement ne se modélise plus en k*v, mais en h*v^2, ainsi la force de frottement est proportionnelle au carré de la vitesse. Les calculs qui en découlent sont beaucoup plus délicats et les équations obtenues n’admettent pas de solution analytique. Autrement dit il faut créer un programme pour obtenir des solutions « point par point ». Le résultat que j’ai obtenu est peu différent du modèle des frottements linéaires, je ne développerai donc pas plus cette partie !
Deuxième partie : Service croisé extérieur
Cette fois, prenons l’exemple d’un service de droitier, de droite à gauche, visant la ligne extérieure. L’étude ne peut plus se faire dans 2 dimensions puisqu’ici la trajectoire va varier également en largeur. Essayons de montrer à quel point un grand serveur est avantagé dans cette situation…
On prendra la référence précédente (1m80, balle frappée à 2m80, à 200km/h, 90 centimètres en avant).
La démarche est similaire au 1er cas, il va falloir cependant rajouter une composante sur la largeur. En d’autres termes, la balle ayant un mouvement sur la largeur (x), la longueur (y) et la hauteur (z), on aura 3 équations (au lieu de 2) pour définir sa trajectoire.
On gardera l’angle alpha pour désigner l’angle initial entre la verticale (z) et la trajectoire. Il faut par contre définir un nouvel angle, désignant l’inclinaison entre l’axe (y) lié à la longueur du terrain, on appellera cet angle beta.
L’origine du repère représente le point d’impact de la raquette avec la balle.
On traitera directement le cas avec les frottements linéaires :
De la même manière qu’au 1er cas, on a les équations de la vitesse projetée sur les 3 axes :
Vx(t) = v0*sin(beta)*exp(-(k/m)*t) (1)
Vy(t) = v0*sin(alpha)*exp(-k/m*t) (2)
Vz(t) = ((m*g)/k – v0*cos(alpha))*exp(-(k/m)*t) – (m*g)/k (3)
La norme de ces trois composantes donne la vitesse réelle dont voici l’évolution au cours du temps :
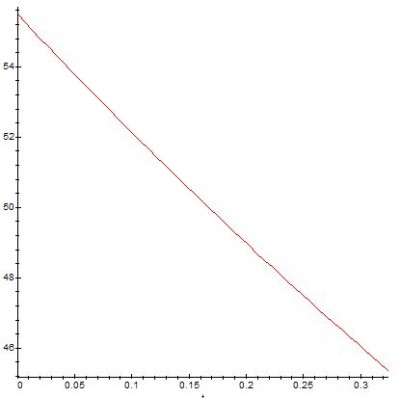La perte de vitesse est très légèrement supérieure au cas précédent, ce qui est logique car la distance à parcourir est un peu plus longue et donc les frottements de l’air agissent plus longtemps.
Voici, sans détails, les équations paramétriques de la trajectoire :
X(t) = -(m*v0*sin(beta))/k*exp(-(k/m)*t) + (m*v0*sin(beta))/k + x0 (4)
Y(t) = -(m*v0*sin(alpha))/k*exp(-(k/m)*t) + (m*v0*sin(alpha))/k + y0 (5)
Z(t) = (m/k)*(v0*cos(alpha) – (m*g)/k)*exp(-(k/m)*t) – (m*g)/k*t + (m/k)*((m*g)/k – v0*cos(alpha))+z0 (6)
Faute d’un logiciel peu représentatif, je ne vous montrerai pas la trajectoire du service (difficile à représenter en 3 dimensions). Néanmoins, les calculs permettent de comparer différents types de serveurs, en l’occurrence on reprendra nos amis Rochus et Karlovic !
Ainsi pour Olivier Rochus servant à 200km/h, s’il veut toucher la ligne extérieure (service idéal !)et passer au-dessus du filet (dont on fixe cette fois la hauteur à 0.999m), on aurait un angle alpha=83,3° et beta=16,6° et la balle atterrirait à une longueur de 17,75m, ce qui est bien dans les limites du court, avec une durée de 339ms.
Pour Karlovic avec les mêmes conditions de service, il toucherait la ligne extérieure avec un angle alpha=79,3° et beta=18,3° avec un impact au sol à 16,05m, soit 1m70 avant le service de Rochus, avec une durée de 305 ms, donc un service 10% plus court en terme de temps que celui du Belge ! Vous imaginez la différence d’effort d’anticipation et d’explosivité pour le retourneur entre ces deux services !
Là encore, l’écart de vitesse à l’arrivée est pratiquement inexistant entre les deux services. C’est donc bien au niveau de la position et dans une moindre mesure, au niveau du temps, que le grand serveur possède un avantage énorme.
Conclusion
Le service a été étudié avec plusieurs hypothèses pour simplifier l’étude, qui m’a déjà pris beaucoup de temps… Les résultats sont pourtant assez réalistes et confirment l’a priori. Reste plus qu’à filmer un serveur, étudier la trajectoire avec un logiciel adapté et confirmer ou non le modèle ci-dessus ! J’espère avoir été assez clair… et pas avoir dégoûté trop de monde !
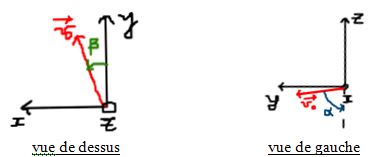
J’ai l’impression que c’est du très lourd ! Je n’ai pas encore lu, seulement parcouru, et je suis malheureusement un allergique aux maths et à la physique… Je salue déjà le travail et je vais essayer d’intégrer toutes ces formules… Bravo d’avance, Benoît !
Et la photo est géniale !
Super, je commenterai plus avant tout à l’heure mais juste qq remarques:
Lorsque Karlovic frappe une première, le point d’impact est à 3,80 m en moyenne..Par ailleurs, 0.9 à l’intérieur du court en moyenne, c’est beaucoup me semble t il..
Tu pourrais visualiser les zones du carré de service que peut théoriquement atteindre un serveur en frappant à plat selon les deux paramètres suivants: la taille du joueur (ou plutôt la hauteur du point d’impact), et la vitesse du service à la frappe..
Oui c’est ce que j’explique dans l’article, j’ai fixé 200km/h mais on pourrait prendre d’autres valeurs..
3m80 tu es sûr ? Ca me parait beaucoup quand même, pour les 90cm, j’ai été peut être optimiste, mais pour un attaquant cela me paraît plutôt raisonnable !
Bel effort! Mais Antoine m ôte les mots de la bouche. Ce qui serait plus parlant ce serait de montrer que karlo peut servir a 220 avec 30 centimètre de marge par rapport a la ligne de carre de service. Surtout de montrer que si Rochus voulait atteindre 210 km/h en plus de devoir s acheter un bras, il devrait servir pile poil sur la ligne. On pourrait même montrer que servir a 240 a plat lui est Physiquement imPossible
Mazette, tu ne serais pas en prépa MP toi??!!
Même si j’en touche pas une sur tes équations, finalement la conclusion est celle attendue: le grand est avantagé par rapport au petit car son service touche plus tôt le sol et est plus court (avantage surtout pour le service extérieur), si j’ai bien compris.
Intéressant
Mazette !!
bravo benoit, tu peux allez déposer un cv pour la série « numbrs »… !!!
waaa, je ne pourrais pas dire que ta démonstration est limpide comme de l’eau de roche, car les maths et moi c’est… euhh juste trop vieux pour que mes neurones aient encore gardé une trace mais tu fais un réel effort pour rendre la démonstration plus abordable que les cours magistraux que tu as du te farcir pour apprendre tout ça !
si j’ai bien compris, plus la balle tombe de haut moins de temps elle met à parcourir la distance au point d’impact ce qui laisse donc moins de temps de réaction à l’adversaire… tu ajoutes à cela les variables comme l’altitude qui accélère ou les effets imprimés à la balle dont tu ne tiens pas compte ici… et on comprend mieux le cauchemar de relancer Dr ivo et big john !
quand cela se joue à la miliseconde, c’est probablement au feeling que tu choisis un côté pour relancer en priant dieu de calculer à ta place où tu dois positionner la raquette !!!
je pense qu’on ne se rend pas bien compte ce que suppose l’effort mental de tenter de trouver la trajectoire parfaite comme la position au retour…
Karlo est un génie de la physique et il ne le sais pas encore !
Excellent Benoît, bon tu triches un poil sur le service au T qui n’a pas non plus une trajectoire rectiligne dans les faits, mais en tout cas tu mets en lumière un truc dont on ne se rend pas forcement compte intuitivement c’est que même pour des services à vitesses égales, le grand est tout de meme avantagé par rapport au petit grâce à ct angle alpha. Je reviendrai commenter encore un peu plus tard !
Bon, j’ai refait les calculs pour le service croisé en prenant cette fois y0=0.5m et non plus 0.9m et dans l’hypothèse où Karlo taperait effectivement la balle à 3.8m (cela me parait quand même assez énorme), on aurait des différences accrues :
Rochus toucherait la ligne extérieure en 349ms et à une longueur de 17,81m tandis que Karlo y serait en 303ms et à 15,46m.
Soit une différence de… 2,35 mètres et une avance de 13% dans le temps pour le géant croate !
@ Concombre : avec ces dernières hypothèses j’ai essayé de voir pour un service croisé jusqu’à quelle vitesse pouvait théoriquement servir Rochus. Réponse : 215km/h. Physiquement il ne peut pas taper plus fort…
Et pour Karlo servant à 240km/h croisé ligne extérieure, il aurait une marge de plus de 2 mètres… Là par contre je pense que le résultat est un peu optimiste..
Ah les frimeurs… « cool article Benoît, super, on apprend plein de choses ».
La vérité est plus nuancée, j’ai les stats (certifiées sofres):
- 83% des internautes avouent ne pas savoir de quoi parle le papier
- 99% disent ne pas avoir lu jusqu’au bout (Antoine est le 1%)
- 71% se sont plaint de troubles intestinaux consécutivement à la lecture
- 44% des personnes interrogées disent qu’elles ont peur de Benoit désormais
- 26% souffrent de conjonctivite
- A la question « que retenez-vous de cet article » nous n’avons reçu aucune réponse
- Ivo Karlovic ne reconnait pas les faits qui lui sont reproché et entend attaquer le site en diffamation.
- Olivier Rochus à la presque-lecture de ce papier a emmené Ivo sur un terrain de volley ball pour tout mettre en perspective. Ivo servait moins bien, comme Rochus sur un court en fait.
Mais au-delà de tout ça, benoît, es-tu un fou?
Moi j’ai lu que le premier tiers et j’ai perdu connaissance. je me suis réveillé dans mon pipi et je retrouve plus mon dentier.
Benoît dans la vie, tu es élève je crois; élève astronaute?
Karim publie des stats, je suis inquiète.
MDR j’ai pourtant essayer de vulgariser un maximum un ptit effort !
Juste un détail sur Rochus. Il est petit mais pas au point de n’atteindre que 2,50m en levant sa raquette. Moi quand je lève juste le bras sur la pointe des pieds j’atteins mon plafond à 2,50m.
Bras + raquette ça fait facilement 1m de plus que la taille, plus l’extension entre 0,2 et 0,4m. Il fait quand même pas 1,20m le Belge.
Benoit, tu t’es bien compliqué la vie en tenant compte des frottements alors que ton étude montre que son impact est en réalité mineur…
Concernant Karlovic, je dis qu’il frappe la balle à 3,80 m de haut mais ceci repose que un article de l’Equipe d’il y a deux ans quand il avait fait un bon parcours à Wimby ou l’on voyait une grande photo de lui et ou ils avaient compté : sa taille, plus le bras, plus la raquette, plus le fait qu’il saute pour arriver à ce chiffre…
Si on simplifie le problème, négligeons l’attraction terrestre et répondons à la question suivante: quelle est la surface de la zone théoriquement atteignable (la « zone utile ») sans toucher le filet selon que la balle est frappée à 2,50 ou à 3,80 m ? Autrement dit, supposons un instant que ce ne soit pas une balle de tennis, mais une balle de fusil ? Cette simplification montrerait que la surface en question est beaucoup plus importante dans le cas de Karlo et dans celui de Rocchus…mais de combien ? C’est ce résulat en termes de surface qui ‘intéresse le plus parce qu’il monterait peut être que cette surface est trois fois plus importante dans le cas de Karlo que dans celui de Rocchus..
Après, on peut raffiner et tenir compte de la vitesse de la balle (pour tenir compte de la gravité) ou des frottements, comme tu l’as fait, mais je suspecte que ces deux paramètres sont du second ordre et ont relativement peu d’impact sur la surface de la zone théoriquement atteignable…Une autre raison de négliger ces deux paramètres est que tu négliges de toute façon ce qui est probablement le paramètre qui a le plus d’impact sur le rétrécissement ou, en l’espèce, l’augmentation de la surface de la zone utile, à savoir que le serveur peut servir kické pour contrebalancer -et au delà – la gravité et augmenter la « zone utile »
Ce serait intéressant que tu précises si tu peux quel est l’ordre de grandeur de l’impact sur la surface de la « zone utile » de ces trois phénomènes: vitesse du service, frottements et effet de kick…
Tu es pardonné pour avoir pris une hauteur de filet pour un service extérieur égale à 0,999 m dans le cas d’un service extérieur. En l’espèce, tu a sans doute pris la moyenne entre la hauteur du filet au centre du terrain (3 pieds (maudits roastbeefs !), soit 0,914 m) et celle du filet sortant du poteau ( 3,5 pieds, soit 1,07 m), ce qui fait 0,992 m..J’observe d’ailleurs que cette hauteur à franchir n’est pas tout à fait la même selon que le service est plus ou moins extérieur, ce qui a un impact sur la surface de la « zone utile » qui est sans doute plus important qu’il n’y parait…..
Je comprend pas trop ton idée de zone utile… La balle est assimilée à un point matériel, donc sa surface n’intervient pas, on considère son centre uniquement. Pour le service croisé, cala consiste à résoudre une équation où l’on fixe l’altitude à 0 (la balle touche le sol) et la largeur (on veut que la balle touche la ligne extérieure pour avoir un service le plus croisé possible), l’inconnue est donc la longueur. En cela le paramètre de hauteur initiale qui varie selon qu’on s’appelle Rochus ou Karlovic va donner une longueur différente, ce que j’ai calculé dans les commentaires précédents.
Oui, il faut simplifier en supposant que la balle est un point…
Mais il ne faut pas seulement calculer la longueur possible (Cf. mon post plus bas), mais également coté regarder le truc en largeur…
La zone utile est un rectangle déformé (un parrallépipède ?) dans lequel le côté extrérieur (celui que l’on touche avec un srervice extérieur) est plus petit que celui situé au centre…
Et cette surface est d’autant plus importante que le serveur est grand bien entendu…
un trapèze rectangle, allez, lâchons nous.
Je pisse de rire en pensant à la tête de Karim quand il va découvrir ce brillant article et nos discussions à ce sujet ! Il va peut être prévenir les services hpospitaliers et essayer de nous faire interner d’office !
Les gars, vous parlez une langue que les filières A (L aujourd’hui) ne peuvent pas comprendre, j’entrave que dalle à vos démos !
Filière B pour moi, mais tout pareil, je touche pas une bille!
Par contre ce qui est super, c’est qu’on voit encore une fois la diversité d’articles qu’on peut avoir sur 15love!
Je vous aime!!!
J’ai essayé hein… Mais je capte rien ! Je comprends l’essentiel en lisant les comm de quelques heureux qui s’y connaissent en maths et formules ! Bravo à eux et à toi Benoît pour ton étude !
Pour faire comprendre la différence de surface théoriquement atteignable par les deux joueurs qui ont des tailles différentes, et en reprenant les chiffres de Benoit:
Pour un service au T, Karlo peut, sans toucher le filet, envoyer une balle qui va toucher le sol au moins 15,61 m plus loin alors que Rocchus, étant plus petit, devra l’envoyer à 17,09 m au moins sous peine d’être arrêtée par le filet si elle est plus courte que cela..
Or la ligne de service est située à 18,29 m de la ligne de fond de court…
Cela signifie donc que Rocchus doit envoyer la balle dans une zone dont la longueur n’est que de 1,20 m alors que Karlovic dispose de 2,68 m, soit plus du double (2,23 fois plus)….
En première approximation (Benoit, tu corrigeras), la surface étant a peu près égale au carré de cette longueur, la zone de « frappe utile » de Karlovic est environ 5 fois supérieure à celle de Rocchus (2,23 x 2,23 = 4,98…)!!!
C’est donc beaucoup plus facile pour Karlo de passer une première balle que pour Rocchus et d’ailleurs, il a un pourcentage de premières qui est très bon. La « zone utile » ou zone atteignable étant très grande, il peut frapper comme un sourd tout en mettant la balle dans le carré de service….
Ça c’est hyper clair.
D’accord je comprend mieux j’avais pas vu l’avantage sous cet angle de surface ! Cela dit tu calcules la surface d’un carré là, alors que la longueur de ton rectangle correpondrait en fait, si j’ai bien compris, à la largeur entière du carré de service. Soit pour Karlo un rectangle utile de 2,68m sur 4,115m (11m^2) et pour Rochus 1,20m sur 4,115m (4,9m^2). On aurait alors une zone de frappe utile non pas 5 fois, mais plutôt 2 fois plus grande…
Je remets un coup sur le trapeze rectangle qui definirait la zone utile, si on prenait en compte la taille du filet qui diminue quand on se rapproche du centre du terrain.
La hauteur n’intervient pas à mon avis puisque l’on cherche seulement un surface.
Non, tu ne saisis pas ce que je dis : la zone utile est une surface définie par quatre côtés :
le premier est la ligne « de fond » du carré de service.
les seconds et troisiemes sont les lignes « de côtés du carré de services. mais ces deux côtés ne sont pas de taille identiques (d’où le trapèze rectangle) car ils sont définis par tes équations. A vitesse égale, comme le flet est plus bas près du T, la longueur ‘physiquement’ accessible pour un joueur d’une taille donnée est plus grande que dans l’angle.
Ce serait plus facile avec un dessin.
L’un des côtés de la surface utile (la longueur utile en cas de service au T) est bien de 2,68 m dans le cas de Karlovic (en reprenant l’hypothèse de l’article sur la hauteur du point d’impact au service). Sa largeur (supérieure) est bien égale à la largeur du carré de service, soit 4,115 m…
L’autre côté du trapèze correspond à la partie de la ligne verticale du carré de service que peut toucher un service extérieur frappé à plat (par hypothèse). Ell est plus petite que 2,68 m pour deux raisons: la première, c’est que le filet est plus haut; la seconde c’est que le filet est plus loin du point de frappe au service…
Le dernier côté réunit les deux points extrèmes des côtés verticaux de la zone de frappe utile: celui situé à 15,61 m (coté T) et l’autre point à déterminer…C’est plus que 4,115 m en tout cas..
Cela ne devrait pas être trop difficile à calculer en négligeant les frotemments et la gravité, non ?
Voilà.
Merci , lis mon com juste en dessous je pense avoir saisi ce que vous vouliez dire.
Ah ok exact on a bien un trapèze dans ce cas. Pas besoin de frottements ou d’attraction c’est que de la géométrie !
J’ai refait les calculs pour un service au T avec les valeurs 3.80m pour Karlo et une frappe en avant de 0.5m.
J’ai ainsi 296ms et 15,11m pour Karlo et 335ms et 17,17m pour Rochus, soit une différence de 2,06m, supérieure à celle calculéée dans l’article et un gain de temps plus faible (11%) !
On calcule ensuite les aires des 2 trapèzes 0,5*(petite base + grande base)*hauteur
avec petite base correspondant au côté ligne extérieure pour le service croisé, grande base au côté ligne centrale pour le service au T et hauteur à la longueur du carré de service (4,115m).
On a : Karlo : 12,36m^2. Rochus : 3,29m^2
Karlovic possède donc une surface de tir 3,75 fois plus grande que celle de Rochus. En clair, il a pratiquement 4 fois plus de chances que le belge de réussir un service à 200km/h….
Voilàààà
Pafait ! C’est exactement ou je voulais en venir..
On voit maintenant ou réside l’avantage déterminant du grand serveur: dans sa taille..
Maintenant, tu peux réintroduire la gravité et les frottements mais cela ne vas pas changer grand chose, je pense…mais accroître l’avantage de Karlovic !
Vous auriez dû faire cet article à trois ce post ci Benoit est beaucoup plus clair que ton article je trouve merci à vous trois j’ai fait travailler mes neurones là
Non cela ne changera rien dans l’étude mécanique donc la zone utile comme tu dis est bien celle trouvée juste avant.
Je ne comprends pas, là Benoit..
Tu as déjà introduit la gravité et les frottements dans le résultat, c’est cela ?
Mais en termes de pure géométrie, cela donne quoi ?
Les calculs de géométrie s’appuyaient sur les petites et grandes bases que je calculais pour chaque serveur, ce que j’ai fait dans l’étude mécanique en comptant le poids et les frottements ! Puis j’ai calculé les aires des deux trapezes.
Ça a l’air vachement bien, mais pour les feignasses dans mon genre, une question: que faut-il retenir exactement ?
La démonstration est tellement brillante que je lui fait entièrement confiance, donc c’est surtout le résultat final qui m’intéresse.
« 71% se sont plaint de troubles intestinaux consécutivement à la lecture »
: je peux témoigner j’en fais partie. Je vous Iphone depuis le trône que je ne quitte plus depuis la lecture de cet excellent article très dépuratif
ça tombe bien j’avais 1 kilo à perdre pour rentrer dans mon maillot de bains !
En plus je lis sur Benoît, ceci : « Benjamin de la rédac’ (11 ans et ½), vu qu’il adore le tennis, il joue… au ping-pong (enfin tennis de table, il faut faire la nuance) : Benoît »
Trève de blague, bravo Benoît.
Bien l’idée et la démonstration ! C’est certain qu’il y a beaucoup de variables en jeu en dehors de la hauteur à laquelle la balle est frappée (surtout les rotations…).
D’accord avec Antoine pour dire que le résultat parlant est en terme de surface atteignable par tes 2 exemples, Benoit. En particulier, c’est la trajectoire proche du couloir qui montre l’avantage énorme au final, en terme d’angle (donc en sortant l’adversaire totalement du court !)
Et dire que Karim m’avait qualifiée de dérangée mentale ou un compliment du même genre avec mon explication sur le glissement de la balle sur gazon
ta pathologie est infiniment plus légère que celle de Benoît. Sois rassurée
En parlant de Karlo, ça nous amène à Kudla, son vainqueur à Newport qui a sorti facilement Dimitrov. C’est Hewitt 2 ce type ?
Benoît, tu es la preuve vivante que l’épreuve du Bac (S forcément) a encore une certaine valeur. Pour ma part, c’est moins vrai. Au bout de 10 lignes j’ai pris une aspirine. À la 20 ème j’ai vomi en récitant la table de 2 et, à la moitié de l’article, le Samu est arrivé. Bel effort cependant pour nous réconcilier avec les maths et la physique. Je n’ose imaginer ce qui arriverait si tu partais en vacances avec Antoine…
Merci Benoit, je me coucherai ce soir en me sentant plus con
Mdr j’avais déjà essayer de résoudre ce problème il y a un an en sortant du bac, mais j’ai pas pu aller assez loin. C’est après un an de prépa que j’ai pu réellement l’avancer !
« C’est après un an de prépa que j’ai pu réellement l’avancer ! »
OK, ça me rassure, t’as bien fait une prépa, c’est pas moi qui est con
Quand tu dis que tu as fait au plus simple, tu avais bien l’intention de te foutre de la gueule des 3/4 de lecteurs du site ayant arrêté leurs connaissances mathématiques au théorème de Pythagore, non? Je ne bite absolument rien au propos (bon j’avoue, j’ai lu l’intro, la ccl et me suis évanoui entre les deux) mais ça a l’air très beau.
La conclusion, c’est bien que Karlovic est plus grand que Rochus? ou tu peux démontrer l’inverse avec des formules mathématiques et physiques prouvant que l’écart de taille entre les deux n’est en réalité qu’une illusion d’optique.
Et beh.. je suis arrive au bout. Heureux.
« j’ai pourtant essayer de vulgariser un maximum »
Benoit 2011
C’est sur que balancer
Z(t) = -((m/k)*((m*g)/k – v0*cos(alpha)))*exp(-(k/m)*t) – (m*g)/k*t + (m/k)*((m*g)/k – v0*cos(alpha)) + z0 (10)
C’est tres vulgaire.
Et si tu nous analysait plutot l’impact du tour de hanches de Serena sur son coup droit?
Non mais ça c’est pas important, c’est les conclusions qui suivent qu’il faut lire ! :=)
Sinon c’est vrai que tu joues au ping?
Oui j’ai fait du tennis et du ping et cela fait 5 ans que je fais du ping !
Vous saviez que Lendl dort avec un cintre dans la bouche ?
Nan mais c’est une blague Benoit!
Je n’en reviens pas. Je sais que 15-LT n’est pas comme les autres sites mais là, la barre est haute.
Ma foi, bravo Benoit!
Ma minable tentative de détournement de sujet tombe à plat …
C’est le homard qui fait pas sérieux, Sam.
J’ai tenté aussi plus haut, mais rien à faire les équations nous tiennent prisonniers. J’ai peur.
Anthologique l’article de Benoît, enfin quelqu’un a réussi à me faire comprendre le pourquoi du comment du mystère du parpaing qui tue, toucher du doigt ma haine de Karlo, donner un sens à mon horreur des gros serveurs.
Ca ne date pas d’hier, çà me renvoie aux misérables 5/20 récoltés en maths toute ma scolarité, mais c’est bon sang bien sûr !!
Enfin, quand je dis que je « comprends », je fais comme tout le monde, je frime.
Parce qu’en plongeant dans l’article pour me coucher moins bête ce soir, le seul truc qui m’a accrochée après une demi-heure d’intense concentration, c’est : « Ce modèle est donc faux ! », … et là, j’ai instantanément revu cette prof de seconde sadique qui nous expliquait (brillamment, en plus !) ce qu’il ne fallait SURTOUT PAS faire pour résoudre nos équations bienaimées. Une sorte d’apprentissage par le vide, la théorie du miroir inversé, du gant retourné, qui la faisait bien rire la sal…eté.
Et ça Benoît, c’est traumatisant !
Mais bon, ok, j’essaierai de le relire une seconde fois ton article, malgré le vieux traumatisme. Et si je n’y comprends toujours rien, je te croirai sur parole.
Parce que tu le vaux bien.
Bravo.
« Ce modèle est donc faux ! »
Et dire qu’avant cette phrase, je me demandais, « mais, la vitesse horizontale ne varie pas dans le temps ? Elle devrait diminuer, non ? ». Du coup, j’ai moyennement apprécié sur le coup. MAIS avant ces quelques mots fatidiques, j’avais compris les équations, ce qui m’a permis d’accrocher au texte. Ça s’est gâté par la suite, je crois que je ne finirai pas aujourd’hui.
Une question à Benoît pour commencer : quelle valeur de coefficient de frottement a été prise ; pour les vitesses indiquées, la force de frottement est proportionnelle au carré de la vitesse mais effectivement, on obtient des résultats convenables comme ça a été fait (si la vitesse varie peu, la force de frottement est quasi-constante).
Pour les services croisés, la méthode utilisée complique le problème qui reste à deux dimensions, la trajectoire étant plane. Il suffit alors d’utiliser Pythagore pour faire varier la distance à atteindre en fonction de l’angle de « croisement », la position du filet correspondante et sa hauteur.
Il faut augmenter la hauteur du rayon de la balle, même si les calculs sont faits pour un point matériel (sauf pour les frottements qui n’existeraient pas).
Bravo pour les calculs en tout cas, tu devrais réussir suptennis l’an prochain.
Le coefficient de frottement, je l’ai calculé grâce à l’équation issue du PFD que j’obtiens. Après un temps très long, comme je l’ai dit la vitesse se stabilise à une vitesse limite d’environ 60km/h. On a alors l’égalité : m*g = k*vlim, m,g et vlim étant connus, on en déduit k..
D’accord pour le rayon de la balle mais cela ne changera pas grand chose aux résultats, et surtout les différences entre les 2 joueurs resteront identiques.
Ouh la la…
Bon je suis censée me remettre aux maths l’année prochaine moi alors ton article peut etre une bonne introduction, je vous rappelle si j’en sors vivante!
Bel effort Benoit ! Mais place à une critique dure mais juste.
1) Le service à plat est un pur cas d’école : à 200 km/h, le moindre effet kické a plus d’influence sur la trajectoire que la pauvre action de la gravité en 0,3 secondes. Juste un problème d’hypothèse qui ne retire rien à ta démonstration.
2) Les frottements sont beaucoup plus fluides (quadratiques) que visqueux (linéaires). Ca c’est grave puisque lorsque la vitesse en sortie de raquette est de 200 km/h, elle n’est plus que de l’ordre de 110 km/h au rebond, à la différence de ton estimation. La réduction de vitesse a son importance puisque elle a pour effet d’augmenter l’effet de la gravité sur la trajectoire et courbe plus celle-ci.
Il faut donc que tu fasses péter un tableur avec un calcul pas à pas, ce que tu trouveras beaucoup plus facile que la résolution des équadifs qui n’est guère plus pratiquée que par les Russes. Tu pourrais en profiter pour regarder l’influence du diamètre de la balle, et des peluches (accrochage de couche limite qui augmente le diamètre apparent et préserve une rotation sans frottements).
3) L’effet est facile à prendre en compte. En première approximation, si la vitesse varie beaucoup sur la trajectoire, la rotation varie très peu (données expérimentales). Le théorême de Bernouilli permet alors de modéliser grosse moto l’effet d’une rotation de la balle comme une pression constante et perpendiculaire au vecteur vitesse. Je te laisse chercher ça ainsi que « effet Magnus » sur le net. En cas de service kické ça agit un peu comme une « super-gravité » qui courbe la trajectoire.
4) Enfin le net présente plusieurs données expérimentales mesurées à la camera rapide sur les trajectoires des services, grâce auxquelles tu peux recaler et crédibiliser tes calculs comme tu le souhaites dans ta conclusion. On trouve aussi sur le net les Cx de différentes balles (le coeff de frottement fluide). Tu verras que la principale différence avec tes conclusions est le ralentissement très important de la balle entre la sortie de raquette et le rebond, et plus encore après le rebond. Un service de Karlovic ne se traine plus qu’à 70 km/h lorsqu’il arrive dans la raquette du relanceur, mais c’es+ une autre histoire.
En tout cas ton article représente un genre tout à fait nouveau sur 15-Love. Bon courage en prepa et n’oublie pas les fondamentaux les plus importants de la vie étudiante : apprendre la guitare, faire beaucoup de sport et enrichir au maximum sa vie sexuelle (j’allais dire sauter un maximum de gonzesses qui correspond bien à ce que j’avais en tête mais la formule retenue en finale me paraît plus générale et prudente).
Oui oui ne t’inquiète pas Ulysse j’ai toujours une vie sociale !
J’ai traité le cas des frottements turbulents. Néanmoins le coefficient de frottement fluide me pose problème car si j’en crois mes résultats, je me rapproche plus d’une trajectoire sans frottements que d’une sans frottements.
Si la perte de vitesse que tu me décris est effective, alors tout mon travail est faux, c’est déprimant ! Bon cela dit je pense qu’au niveau surface de frappe et écarts entre Rochus et Karlovic, on devrait obtenir des résultats assez similaires. Je n’ai pas encore vu l’équation de Bernouilli !
Ouarf ! Ulysse, tu me tues : « Le théorême de Bernouilli « ….si demain j’arrive à placer ça dans une conversation, mon aura sociale en sera sans nul doute multipliée par 12.
Si tu te mets à citer le théorême de Bernouilli dans les conversations, il est possible que ton aura sociale évolue, mais ta vie sexuelle va ressembler au désert de Gobi.
J’aime beaucoup les maths, beaucoup moins la physique. Je ne sais donc pas si je vais avoir le courage de lire ce soir vu que j’ai regardé (attentivement) des chiffres toute la journée mais j’adresse déjà un merci à Benoit pour s’être attelé à ce sujet qui m’a l’air très intéressant.
« 15-Love », « vie étudiante » et « vie sexuelle ». Je comprends maintenant pourquoi je ne loupe quasiment jamais les posts d’Ulysse.
Pourrions-nous avoir la contribution d’un nain sur la question ?
Hmmm ? Avis aux posteurs.
Miam, un petit retour en prépa. Ca pourrait être un sujet de concours sympa, ça nous changerait des grains de sable qui s’entrechoquent et des grues en tous genres…
Une petite remarque sur l’article : Je ne comprends pas bien comment il peut y avoir un gain de temps réel pour Karlovic contre Rochus. A priori le service tombe de plus haut (donc a plus de distance à faire) et va grosso modo à la même vitesse. La différence de durée ne serait-il pas du à la différence de distance d’impact ? (Karlo touche le sol avant donc moins de temps)
J’ai lu l’article rapidement car je suis un peu claqué donc si je raconte n’imp ne m’en veux pas.
Et sinon pou l’effet Magnus il n’y a que ça de vrai ! Ou l’utilité de lifter comme un porc pour éviter le filet ^^
C’est simple. Karlo tape 1,3m au-dessus de Rochus. La pression atmosphérique à cette altitude est réduite. Intégrons l’équation d’équilibre de l’atmosphère : DP = rho g dZ avec Rho=1.3g/l, g=9.81 m.s-2, dZ=1,3m. On peut exprimer l’âge du capitaine en fonction de la vitesse du vent. On intègre en coordonnées sphériques sans oublier le jacobien et on simplifie en utilisant l’intégrale de Gauss, puis la formule de Green-Ostrogradski. En résumé, Karlo est tellement grand que c’est comme s’il servait en atmosphère raréfiée à Mexico. Par équité on devrait tenir compte d’un coefficient correctif dans le calcul de ses points ATP, ou bien demander aux joueurs de taille H de servir depuis (H-Hrochus)/22,31 derrière la ligne de fond.
Excellent !
La deuxième option me plait bien, les retours amortis pleuvraient
Ouais ben va amortir une première balle de karlovic et on en reparle.
Tu sais que vers 2001 l’ATP a sérieusement étudié le rajout d’une petite ligne de service 50cm à 1m derrière la ligne de fond pour amoindrir l’emprise étouffante des serveurs fous sur le top niveau ?
Finalement ils ont préféré pousser les tournois à ralentir les surfaces et surtout l’ITF a mis en place des balles plus grosses sur dur dès 2002, solution moins chère à l’investissement et dont curieusement on a entendu parler très peu.
S’il est plus loin, il doit servir moins fort, non ?
« Tu sais que vers 2001 l’ATP a sérieusement étudié le rajout d’une petite ligne de service 50cm à 1m derrière la ligne de fond pour amoindrir l’emprise étouffante des serveurs fous sur le top niveau ? »
Heu, non, je ne savais pas. Ça aurait été compliqué à faire passer puisque c’est forcément arbitraire, ça me fait penser aux tranches de revenus pour le calcul des taux d’imposition.
Je me suis exprimé avec ambiguïté. Cette ligne supplémentaire aurait été valable pour tout le monde bien sur.
« En réalité l’atmosphère crée une 2ème force, de frottement, qui s’oppose au déplacement de la balle »
-> En réalité, il y a en même une troisième, la poussée d’Archimède dan l’air…
Oui, je suis déjà dehors, ne vous fatiguez pas.
Certes, mais cette force est largement négligeable dans l’air
Et la force de Coriolis ? Et l’effet Casimir ? Et la précession des équinoxes ? Et est-ce que Karlo peut servir si vite, que par effet Doppler relativiste sa balle devient verte vue du relanceur et se confond avec le gazon ? Et est-ce que Karlo peut servir à travers le filet par effet tunnel ? Et où est-ce que j’ai rangé ma bouteille de Laphroaig ?
L’effet tunnel je sais même pas ce que c’est, par contre. > <
C’est quantique. Expliqué très mal avec les mains ça donnerait ça : quand on va très vite, le mouvement, la position d’un objet comme toute autre quantité physique n’est pas continu mais occupe des valeurs discrètes. Pour la balle on peut imaginer une valeur discrète de sa position avant le filet, puis la valeur discrète suivante après de telle sorte qu’elle le traverse sans jamais le rencontrer. On le fait bien avec des électrons…
De toute façon, sans les corrections relativistes, ce modèle est clairement incomplet! Vu le masse de Karlovic, on ne peut décemment utiliser la gravitation de Newton et il est nécessaire de passer a la relativité générale. Et comme le dit Ulysse, les corrections quantiques sont fondamentales, et il faut donc utiliser une théorie relativiste quantique de la gravitation… et la seule de ce genre disponible aujourd’hui (et qui en plus est supersymétrique), c’est bien la théorie des cordes.
Or, de quoi est fait une raquette de tennis? DE CORDES !!!
Coïncidence? I think not! Clairement, on voit ici que rien n’est laissé au hasard et que tout a un sens! Car Doudou == diminutif de Edward ! Et qui est le grand maitre des cordes, et de la theorie M (M comme Meilleur joueur de tout les temps?) ? Edward Witten (http://fr.wikipedia.org/wiki/Th%C3%A9orie_M)
Et donc (et la pertinence de ma demonstration m’eblouie moi-meme), Roger est donc bien le GOAT, sans discussion possible, comme on vient de le voir scientifiquement.
La théorie des cordes c’est has been. Moi c’est bien simple : je ne l’utilise jamais.
Ah dis Florent, c’est imparable. Heureusement que je n’ai pas de fille parce que sinon je saurais pourquoi elle est muette !
merci de nous ramener un peu vers les belles lettres.
Bravo Professeur Benoit pour tes analyses scientifico-tennistique.
J’ai pas tout compris mais ce que je retiens c’est que visuellement comme mathématiquement, les géants sont avantagés au service.
Pardon d’avance pour cette question mais on ne peut prendre en compte la vitesse sans faire mention de la puissance ou la force si?
Isner et Karlo ont 2 cms d’écart, j’imagine que ta démo serait équivalente ou presque pour les 2 mais que se passe t’il si la vitesse parcourue n’a pas la même accélération?
L’accélération est liée aux forces qui s’exercent sur la balle par le principe fondamental de la dynamique. Ainsi en découle la vitesse. La puissance c’est autre chose par contre !
« que se passe t’il si la vitesse parcourue n’a pas la même accélération ? »
A force de concentration et d’imagination, je ne vois toujours pas ce que tu veux dire par cette question, et c’est surement mon effort mental le plus important depuis quelques années.
L’analyse de Benoît commence en sortie de raquette mais n’aborde pas ce qui se passe avant.
La puissance intervient dans le profil du contact raquette / balle qui au moyen d’un choc, accèlère la balle pour lui confèrer une certaine vitesse initiale. Ce n’est pas un paramètre important dans un choc élastique, il vaut mieux considérer son intégration dans le temps qui est l’énergie. L’énergie d’un service de Karlo peut atteindre plus de 130 Joules transférés en 0.014s au moment de la frappe soit une puissance de transfert de 9000W. C’est là où on voit que le geste et le matériel sont réellement très sophistiqués pour focaliser autant d’énergie en un temps si court. Lance Armstrong développe lui 480W, mais pendant toute la montée de l’Alpe d’Huez.
Je voulais savoir si 2 joueurs servent tous les 2 à 200 km/h (à vitesse égale) si la balle pouvait avoir une accélération différente selon le joueur (point d’impact, rotation, angle…), c’est plus de l’ordre de la cinétique je pense.
Peut-être que cela n’entre pas en ligne de compte effectivement, car la vitesse du service est calculée lorsque la balle quitte la raquette et non durant la distance parcourue.
N’empêche que ce facteur doit avoir une certaine influence sur le service.
T’as pas tout compris mais tu réponds presque à ma question
Je vois que Gasquet a amorcé sa marche vers la victoire.
Oui elle sera différente puisqu’avec les frottements l’accélération dépend de la vitesse et du poids. Le poids est invariant puisque la masse de la balle ne change pas (sauf si Karlo se met à servir à 30 000 km/s, auquel cas on devra traiter le problème en relativité…). Or la vitesse de la balle à son impact au sol est légérement supérieure pour un grand serveur car la durée du service est un peu plus courte (cf l’article), donc l’accélération juste avant l’impact sera légèrement supérieure pour Karlo, mais l’écart est très très faible…
M. Rectitude et Génial olivier, do you remember ? Faîtes quelque chose, là, ça part gravement en vrille !
Échanges mythiques suite a cet article, et particulièrement les corrections du problème par Tonton Ulysse et ses recommandations pour réussir une bonne prepa (guitare, sport, sexe). Avec ces conseils, tu es pare, mon cher Benoit, essaie d’alterner Bernoulli et Baisoulli pour garder la tête froide
Alors j’ai pris le temps de bien relire l’article et les commentaires, décidément très intéressants tout ça.
J’ai pas la prétention de rajouter des éléments sur le fond dans la mesure où je n’ai pas du tout un cursus scientifique, même si je garde une forte « affinité intellectuelle » on va dire avec les maths, et que les illustres Antoine et Ulysse font ça beaucoup mieux que moi de toute évidence ! Par contre certaines conclusions et étapes du raisonnement m’inspirent quelques réflexions.
Si, comme le dit Benoît dans son com plus haut, on considère que Karlovic a quasiment 4 (disons 4 pour simplifier) fois plus de chances que Rocchus de mettre un service à 200 km/h dans le carré, que disent les faits ? Je me doute que ça doit pas être facile (et même probablement impossible) de trouver de telles stats, mais on doit s’attendre à ce qu’en servant à cette vitesse Karlo passe sa balle 4 fois plus fréquemment que Rocchus (en prenant en compte toutes les hypothèses de départ bien sûr). En gros il faudrait prendre un échantillon de services frappés à plat à 200 par Karlo, la même pour Rocchus, et faire le ratio de leurs pourcentages de réussite pour voir si on tombe bien sur un rapport de 1 à 4…
D’autre part je constate que 40 centimètres séparent le grand Croate et le petit Belge pour un « avantage pur » de 1 à 4 donc, mais comment évolue cet avantage en fonction de la taille ? En gros, si Karlo faisait 60 cm de plus, on aurait quoi, une surface utile 6 fois plus grande ? Ou plus ? Ou moins ? Y a-t-il une taille limite à partir d e laquelle l’avantage disparaît parce que la distance à parcourir par la balle est trop grande car tombant de trop haut (pas en termes de surface utile du coup, mais en termes de vitesse peut-être) ?
Autre chose, la conclusion à retenir est que le serveur est avantagé par une grande taille (qui lui permet d’atteindre des zones que ne peut atteindre quelqu’un plus petit), mais est-ce que la masse du serveur peut également augmenter son « avantage pur » ? Intuitivement j’aurais tendance à dire non, une idée ?
Dernier point, en revenant sur ce rapport de 1/4, et en supposant qu’il ne soit pas corroboré par les stats (supposons qu’on ne trouve qu’1/2 dans les faits), on pourrait alors dire en tirant le trait que… Rocchus est un serveur deux fois meilleur que Karlovic non ?? Non pas qu’il a un meilleur service, mais bien qu’il est un meilleur serveur…
Ça serait assez marrant de constater un truc pareil !
Bon désolé si je manipule mal les notions et les termes, j’ai un peu l’impression de me noyer dans ma bave pour être honnête alors si un des authentiques scientifiques ici présents veut bien venir à ma rescousse et me dire que je raconte n’importe quoi (ou pas) c’est avec plaisir !
La probabilité de réussir une première balle dépend forcément de la surface (plus exactement l’angle solide) de carré de service visible depuis la balle au moment de l’impact. Mais ce n’est qu’un des facteurs. Le serveur peut « courber l’espace » en transférant une partie de l’énergie dans le kick plutôt que dans la frappe à plat. La gestion de ce partage entre effet et frappe à plat permet à tous les joueurs d’avoir à peu près la même probabilité de réussite en première balle (sauf Richie en CD pour qui les lois de la physique ne s’applique pas, où n’ont pas le temps de s’appliquer, … enfin bref on sent que la nature consulte son bouquin à son sujet et hésite sur la bonne façon de transformer la force en accélération).